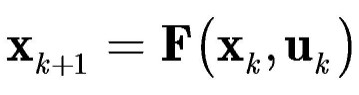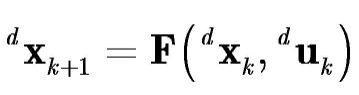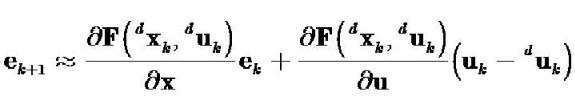BACKGROUND

Proportional control valves are widely employed for motion control in hydraulic applications. The advantages of poppet valves over spool type valves in proportional control applications include a higher resistance to contaminants, less faulting, high flow area to poppet displacement ratios, excellent sealing capabilities, low cost and maintenance, and less strict machining tolerances.

A novel type of proportional flow control valve is manufactured by HUSCO International. These are referred to Electro-Hydraulic Poppet Valves (EHPV) (US patent No. 6,328,275 and 6,745,992.) The flow control of hydraulic fluid through the valve is achieved by changing the valve conductance coefficient, Kv, via a pulse-width-modulated (PWM) input current acting on a pilot and a poppet type orifice with patented pressure compensation (US patent No. 5,878,647.) The flow control feature and the integrated electronics of the EHPV enable the implementation of advanced control algorithms and further extend the valve capabilities to more applications.

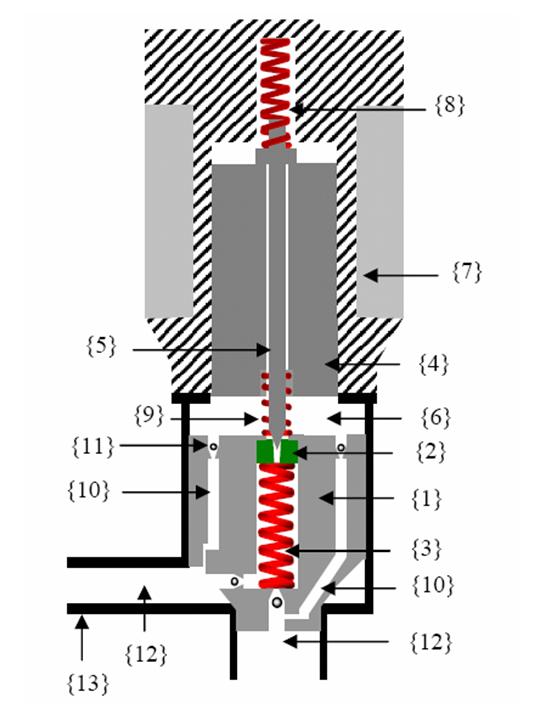A detailed explanation of the functioning of a single EHPV is explained next. The first stage of the valve includes a main poppet element {1} and a pressure compensation mechanism consisting of a compensating piston {2} and a tubular spring {3}. The second stage houses an armature {4} and a pilot pin {5}. A control pressure chamber {6} separates these two stages. In order to achieve flow through the valve, high-pressure flow (inflow) is conducted through a small passage {10} in the main poppet to the control chamber. When the solenoid {7} is activated, the pilot pin is pulled and fluid is allowed to go from the control pressure chamber through the piston and tubular spring to the low pressure side. Such action lowers the pressure in the control pressure chamber. By lowering the pressure in this chamber, a pressure imbalance is created across the main poppet that enables the displacement of the latter away from the valve seat and hence a direct passage between the inlet and outlet connections of the valve is established. The bidirectional capability of the valve resides in the fact that the control pressure chamber receives the high-pressure flow from either port of the valve. Other components of the EHPV include a bias spring {9}, check valves {11}, the inlet and outlet connection ports {12}, and the valve cartridge {13}.

For motion control of hydraulic actuators, four (4) EHPV's are used in a Wheatstone type of arrangement, as shown next.

The fact that each valve can be controlled independently (independent metering), several metering modes are achievable.

High side extend (HS_EXT)

High side retract (HS_RET)

Standard extend (STD_EXT)

Standard retract (STD_RET)

Low side extend (LS_EXT)

Low side retract (LS_RET)

 Other advantages include:

        1. More degrees of freedom

        2. More efficient operation

        3. Simple circuit

        4. Distributed system

        5. Ease in maintenance

HUSCO International has created a novel type of control algorithm to be employed with the EHPV's for motion control of hydraulic cylinders called INCOVA (INtelligent COntrol VAlve). This algorithm is used to compute the individual valve openings (Kv) given a commanded velocity signal a from a human operator, and the relevant system pressures. When these opening values (Kv) are known, individual valve's look up tables are used in an open-loop manner to command current signals that in turn individual valve current servos deliver to each valve solenoid. For more details consult US patent No. 6,732,512, or the following papers:

[1] Tabor, K., (2005), "Optimal Velocity Control and Cavitation Prevention of a Hydraulic Actuator Using Four Valve Independent Metering", in Proc. SAE Commercial Vehicle Engineering Congress and Exhibition.

[2] Tabor, K., (2005), "A Novel Method of Controlling a Hydraulic Actuator with Four Valve Independent Metering Using Load Feedback", in Proc. SAE Commercial Vehicle Engineering Congress and Exhibition

RESEARCH MOTIVATION AND CHALLENGES

Currently, the opening (conductance) of each EHPV is controlled via open-loop. This is accomplished by electronically adjusting the valve’s Kv with the aid of fixed lookup tables. In order to accurately determine the required input for open-loop control, the relationship between the solenoid current and the valve’s Kv is obtained via offline calibration for both flow directions (bidirectionality).

The motivation for this research is then to improve this process and have feedback control of EHPV’s.

It is important to mention that Feedback control could be a better alternative to open-loop control, but it would require the use of a sensor to provide the actual or estimated Kv value. In many applications, adding hardware (in this case a dynamic flow meter) to implement the feedback control law is cumbersome and expensive.  Currently, feedback of the actual valve opening is unavailable in some construction machinery (excavators for example).

The challenge is then to develop intelligent control technology capable of learning online (i.e. while in operation) both the steady state characteristics and transient behavior of the component at hand along with improving its performance. The challenge also resides as to how the learning part can be accomplished efficiently. As such, adaptive lookup tables give an attractive solution to the control problem, especially for the inverse input-output mapping learning approach. The inclusion of adaptive lookup tables in the control task enables the online learning of the dynamic behavior of such complex systems. Particularly, adaptive lookup tables can be updated by perceptron neural networks which are preferred for their simplicity and for their capability to approximate and store complex nonlinear functions with the ability to self-adapt to reflect the system’s changes that might arise as a result of prolonged operation. Moreover, they can be used in such a way that they learn the corresponding control input required to follow a desired state trajectory without the need to explore the entire inverse plant dynamics map, saving memory and effort.

There are three major advantages of doing this: first, there would be no need of having extensive individual calibration, for a nominal mapping from a generic component can be used for similar components and the errors are left to be learned and corrected while in operation (fine tuning). Second, the component’s performance can be improved by combining feedback control with learning the true transient and steady state characteristics, so that the system does not have to be engineered ‘sufficiently fast’. Third, by knowing how the component is truly behaving while in operation, a maintenance scheduling can be implemented from monitoring and detecting the deviations from the normal pattern of behavior

RESEARCH OBJECTIVES

The research objectives are outlined and organized into theoretical and experimental categories. Critical performance issues in the theoretical framework to be addressed are

Development of a general formulation for control of nonlinear systems with parametric uncertainty, time-varying characteristics, and input saturation

Development of a formulation for auto-calibration of nonlinear systems

Study of online learning dynamics along with fault diagnosis

Improve flow conductance control of EHPV’s

Critical experimental performance issues that must be addressed in applying the general control methodology developed herein are

Analysis and validation on the effectiveness of the proposed method

Study of the accuracy of the auto-calibration method

Development of computationally efficient algorithms

Development of a nonlinear observer for state estimation for unmeasurable states

CONTROL LAW

The theory and experimental validation for this research are related to the following control law,

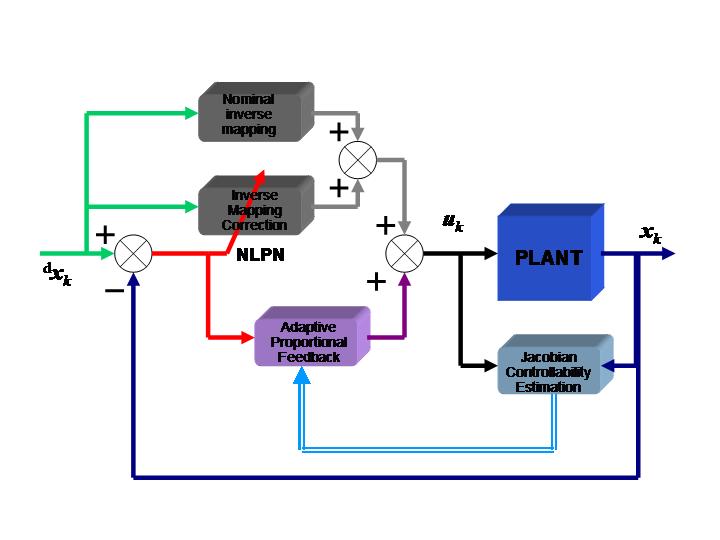
This control law is derived from the following principles.

Given a discrete-time system

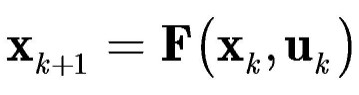
and the desired state trajectory

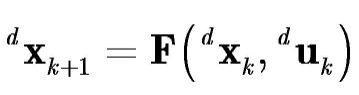
Then, the discrete-time system can be linearized about the desired state trajectory, and the state trajectory error (defined as e_k = ^dx_k - x_k) is then given by

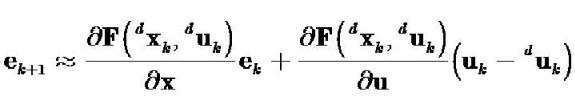
For simplicity, the following definitions apply. (Note: ^dJ_k is known as the Jacobian, and ^dQ_k is known as the Controllability matrix).

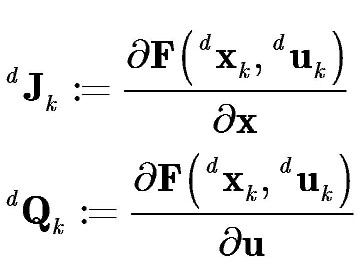
Substituting in these definitions, the state trajectory error is then given by

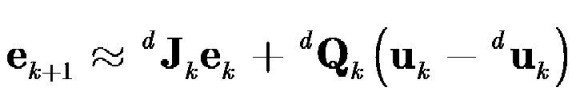
The control law is then formulated as deadbeat control:

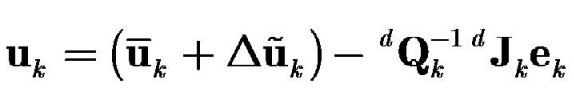
However, for this research the Jacobian and the Controllability matrices are unknown. Hence, the main research effort will be concentrated as to develop the theory about the closed loop stability by employing the estimates of these matrices:

With respect to the figure showing the control law, the "nominal inverse mapping" is given by the first term inside the parenthesis, the "NLPN" (Nodal Link Perceptron Network, a neural network functional approximator) is given by the second term inside the parenthesis, while the "Adaptive proportional feedback" component is given by the leftover terms.